Partial Derivative Equations

01 Sep 2025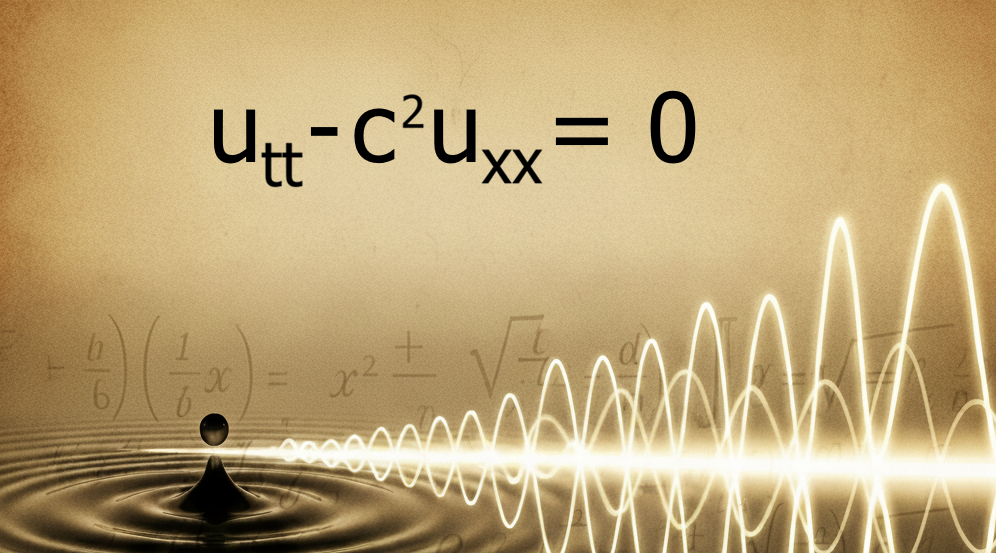

I’m getting ready for my last exams, then my thesis, then I’ll be off! It was a long time, I’m going to accomplish probably the biggest goal I let floating around for years because of ADHD - I’m pretty excited, the last rush is always the hardest but, in some way, I rewired myself to make me able to see the end of the line and it’s nice. To see the end of the line getting closer, I mean. And the subject I’m studying, of course, they relate to my favourite branch of maths: geometry and systems dynamics.

PDE

One of the two exams I’m getting ready for is about partial derivative equations (PDE):

• take a space
• take an item that defines any measures you want about each point in that space. Call the item $u$.
• map how moving in one direction changes values in the item
• link changes in one direction to changes in a different direction: “if I move two steps north and one east the values of $u$ stay the same”

and that is a PDO. Sort of. An easy one, that writes off something like

\[u_N-2u_E=0\]

“What’s the use for that?” - of course. Well, let’s say that instead of “North/South” and “East”, one of the directions can be “past/future”, “East/West” can refer to any positioning and the speed at which you have the changes can be called $c$ and not just 2: you get something like

\[u_t-cu_x=0\]

and you get an equation that represents something that moves in your direction with speed $c$. You can complicate a bit things: instead of saying how much you are moving into a direction, you can say at what rate you increase the speed in that direction. You end getting something like this

\[u_{tt}-c^2u_{xx}=0\]

that represents something in every direction with speed $c$. Like a lightwave. And if you say that in that space there is a source that produces light, then you get

\[u_{tt}-c^2u_{xx}=f(x,t)\]

with $f(x,t)$ an item, like $u$ that says that in a specific position $x$ at the time $t$ a lightwave is produced. You can also slow down a bit and try to match two different levels, like how does speed changes in time. Like if you are watching a drop of ink diffusing in a bowl of water - or heat diffusing into a body, or, reversing time, particles concentrating because subjected to gravity, you end up with something like

\[u_t-Du_{xx}=0\]

And, in the end? In the end the system reaches some sort of balance, where the variations of the system stay stable. So, variations of the variations are 0. Meaning

\[\nabla\cdot\nabla u=0\]

with that triangle being the sum of variations in every direction, also written

\[\Delta u=0\]

with $\Delta$ being called Laplacian operator from Pierre Simon Laplace - interesting guy.

Laplace

Born from a wealthy family, he studied to become a priest, then he studied math and changed his mind. He asked for a letter of recommendation to be admitted to study with D’Alambert, a big name of the time. D’Alambert ignored the letter and him altogether. So Laplace sent him a 4 page essay about newtonian mechanics, to which D’Alambert replied something like “This is a good letter of recommendation, not the garbage you sent me before. Can you start on monday?” (Ok, probably not exactly these words, but that was the idea, pretty much. That’s more often than not why everyone is uncomfortable to work with mathematics but mathematics)

With D’Alambert (which, to be honest, was quite spot on on the second type of equations, so much that these equations are usually written as $\square u=0$ where that square $\square$ is called Dalembertian operator - but I’m digressing) Laplace discovered a lot about dynamic systems and wrote a lot about planets’ movement - he kind of set the standard on the study of dynamic systems, with Lagrange. He was quite the name. And he knew. And he didn’t make really a mystery of that, he thought he was the best french mathematician of his time. That leaves a mark on your reputation if you are not right and let’s just say it didn’t really leave a mark. At the time. Later on a bit, since he used his own status to take some results of other brilliant mathematicians as his own. I’m kinda sure about Fourier, I’ll check that out later.

Fun facts

Napoleon confronted him (Laplace had a job in his government court) saying that Newton referred to God multiple times in his writings while Laplace didn’t. Laplace answered that “he didn’t need that hypotesis”. That answer is still a point of discussion: for someone it frames him as an atheist, for others it frames him just as kind of a dick. I’m slightly more in agreement with the others :)

At his death they removed his brain and kept it in a jar for some time. And it was smaller than average. Maybe it’s a case of “It’s not about the size, it’s about how you use it”. Maybe it’s just a rumor from someone who Laplace pissed of. I mean, there was no scarcity of them.

Whatever. I’ll better go back to study!